
One hardly ever uses Fourier sine and cosine transforms. This analysis can be expressed as a Fourier series.The fast Fourier transform is a mathematical method for transforming a function of time into a function of frequency.
FAST FOURIER TRANSFORM SERIES
We can write f(k)fc(k)+if s(k) (18) where f s(k) is the Fourier sine transform and fc(k) the Fourier cosine transform. Fourier analysis of a periodic function refers to the extraction of the series of sines and cosines which when superimposed will reproduce the function. Several numerical examples axe used to illustrate the efficiency of the approach, and to compare the performances of the two sets of nonuniform FFT algorithms. For a general real function, the Fourier transform will have both real and imaginary parts. These include an efficient version of the Fast Multipole Method in one dimension and fast algorithms for the evaluation, integration and differentiation of Lagrange polynomial interpolants. Several related algorithms are also presented, each of which utilizes a similar set of techniques from analysis and linear algebra. The number of arithmetic operations required by each of the algorithms is proportional to N dot log N N - log1epsilon, where epsilon is the desired precision of computations and N is the number of nodes. Computes the Discrete Fourier Transform (DFT) of an array with a fast algorithm, the Fast Fourier Transform (FFT). These schemes are based on combinations of certain analytical considerations with the classical fast Fourier transform, and generalize both the forward and backward FFTs.

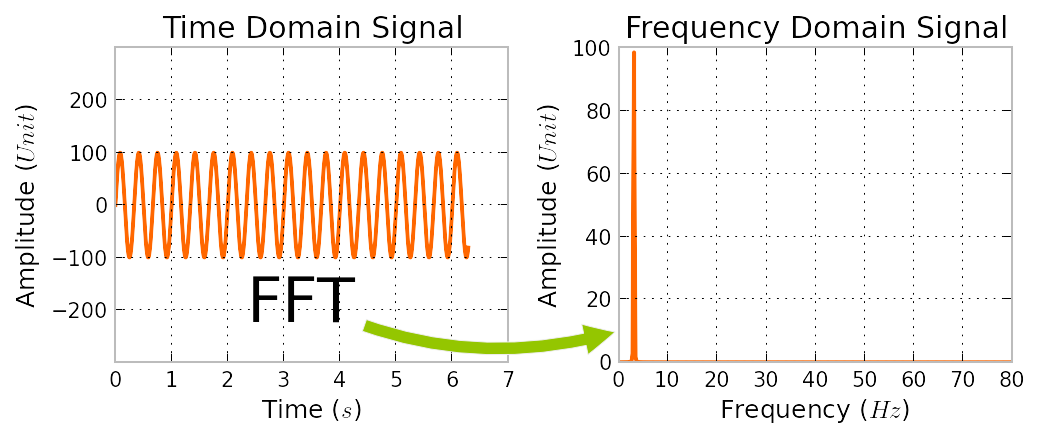
Two groups of algorithms are presented generalizing the fast Fourier transform FFT to the case of non-integer frequencies and nonequispaced nodes on the interval -pi, pi.


 0 kommentar(er)
0 kommentar(er)
